Ну тогда ещё для двадцатого рисунка можно добавить ответ - 1 прямоугольник, потому что он там реально 1, а какой-то дурик туда в него знак вопроса вписал. ))) Тоже ответ. Просто если эта задача с конкретным ответом, то ответ должен быть единственным. Иначе же это такой тест на логику и сообразительность, который тоже имеет право на существование.в том то и дело, что можно посчитать в третьем вопросе и 3 и 4 и 6 - всё зависит от уровня познаний, пространственного мышления и условия задачи
Задачка по математике. 3 класс.
попробуем решить :)
- John Prick
- Сообщения: 9367
- Зарегистрирован: 12 янв 2006, 19:30
- Благодарил (а): 431 раз
- Поблагодарили: 312 раз
- Контактная информация:
Re: Задачка по математике. 3 класс.
-
Мистер Смитт
- Сообщения: 14072
- Зарегистрирован: 17 мар 2008, 11:27
- Настоящее имя: Олег
- Откуда: Смоленск
- Благодарил (а): 0
- Поблагодарили: 0
- Контактная информация:
Re: Задачка по математике. 3 класс.
... просто напиши решение этой задачи, не ответ а решение, как ты решалJohn Prick писал(а):Просто если эта задача с конкретным ответом, то ответ должен быть единственным. Иначе же это такой тест на логику и сообразительность, который тоже имеет право на существование.
... во всём виноват Вашингтон поц ...
... следуй своей дорогой и пусть люди говорят всё что угодно ...
... следуй своей дорогой и пусть люди говорят всё что угодно ...
- John Prick
- Сообщения: 9367
- Зарегистрирован: 12 янв 2006, 19:30
- Благодарил (а): 431 раз
- Поблагодарили: 312 раз
- Контактная информация:
Re: Задачка по математике. 3 класс.
Ну что, опять?!просто напиши решение этой задачи, не ответ а решение, как ты решал
Я считаю все прямоугольники, т.е. у меня однозначно на первом - 1, на втором - 3, на третьем - 6. Четвёртый будет разделён (по самой напрашивающейся идее) тремя линиями, значит прямоугольников на нём будет - 10. 20й будет разделён 19ю линиями... Считать там прямоугольники вручную - дело неблагодарное, поэтому ищем вариант попроще. При должном внимании он находится:
п1) 1 = 1;
п2) 3 = 1 + 2;
п3) 6 = 1 + 2 + 3;
п4) 10 = 1 + 2 + 3 + 4;
...
п20) ? = 1 + 2 + 3 + ... + 20;
Задача упростилась, можно уже и посчитать, чему равено кол-во прямоугольников на 20м рисунке.
Однако можно пойти и далее (ваще на отлично): 1 + 2 + 3 + ... + 17 + 18 + 19 + 20 = (1 + 19) + (2 + 18) + ... + (9 + 11) + 10 + 20 = 9 * 20 + 10 + 20 = 210.
Собственно, всё.
-
John Watson
- Сообщения: 2657
- Зарегистрирован: 07 май 2010, 00:04
- Благодарил (а): 0
- Поблагодарили: 0
Re: Задачка по математике. 3 класс.
Это правильный ответ, по мнению составителя данной задачи.John Prick писал(а):... 1
... 3
... 6
... 210
Re: Задачка по математике 3 класс
На рисунке явно изображён тетраэдр. Соответственно - четыре треугольника. Заметил ли кто-нибудь это? Хотя, если быть до конца честным, то здесь восемь треугольников. Потому. что внутри тетраэдра встроен ещё один тетраэдр - меньших размеров, но его не все видят из-за непрозрачных боковых граней основного тетраэдра. изображенного на рисунке. И так. правильный ответ - восемь. Единственно, что неправильно - это задача не для третьего, а для четвёртого класса.Dms писал(а):Перед началом теста:
-
Storm
- Сообщения: 4784
- Зарегистрирован: 19 ноя 2004, 11:44
- Откуда: Smolensk
- Благодарил (а): 0
- Поблагодарили: 3 раза
- Контактная информация:
Re: Задачка по математике. 3 класс.
На рисунке явно изображён тессеракт. Ну как изображен, как может 3-и класник, так и изобразил.На рисунке явно изображён тетраэдр.
- Aml
- Сообщения: 16662
- Зарегистрирован: 23 окт 2004, 00:10
- Настоящее имя: Сергей Амелин
- Откуда: Смоленск, Николаева
- Благодарил (а): 1 раз
- Поблагодарили: 59 раз
Re: Задачка по математике. 3 класс.
По поводу треугольников. Тут были споры, как считать... Что-то на меня тоска напала, я написал подробный разбор задачи. Итак, что имеем?

Анализируем рисунок.
По каким правилам подсчитываются треугольники:
1. Треугольник формируется из трех отрезков (эти отрезки выделены на поясняющем рисунке справа). Они формируют три стороны треугольника.
2. Внутри треугольника могут быть другие треугольники (пример – большой треугольник)
3. Подсчитываются всё возможные треугольники. Этот вывод делается на основании того, что в поясняющем рисунке подсчитаны именно все возможные треугольники (там всего три возможных, три посчитаны)
Теперь переходим к задаче.
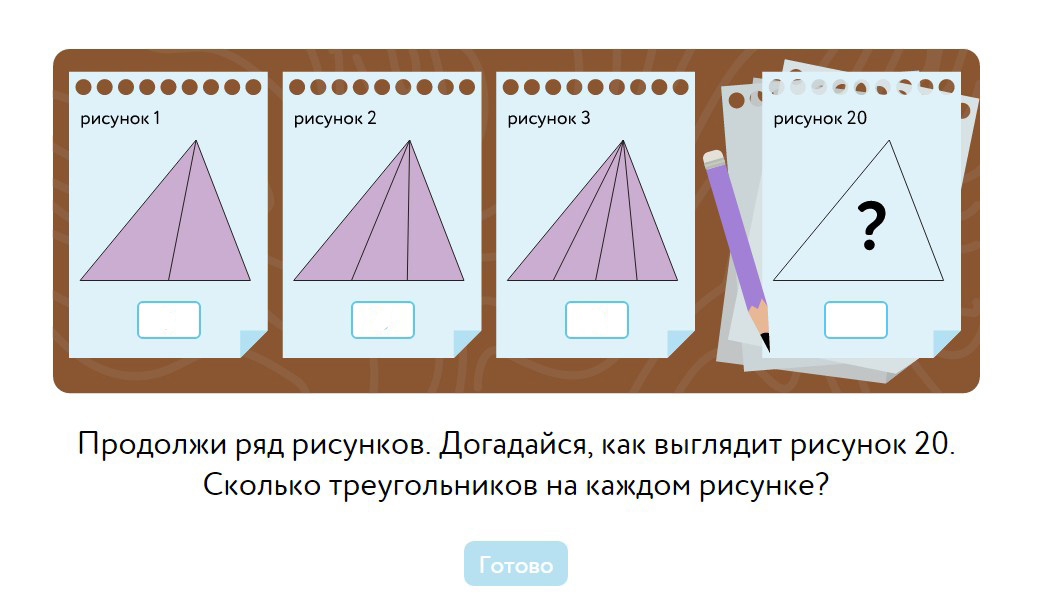
Очевидно, что трем сформулированным выше правилам нужно подсчитывать треугольники на остальных рисунках (рис. 2, рис. 3, рис. 20). Ручной подсчет перебором на 20-м рисунке, в принципе, возможен, но очень трудоемок и за отведенное время явно не реализуем. Нужно сначала на основании первых сравнительно простых случаев увидеть эту закономерность.
Сначала проанализируем три первых рисунка выявить закономерность и понять, как будет выглядеть 20-й рисунок. Определим, что меняется. Внешний контур не меняется. Цвет не меняется. Убираем всё, что было постоянно и остается разница. Вывод: первый, второй и третий рисунок отличаются исключительно числом отрезков, соединяющих вершину треугольника с противолежашей стороной. Никаких других отличий нет.
Рис. 1 – 1 отрезок, рис. 2 – 2 отрезка, рис. 3 – 3 отрезка. Соответственно, на рис. 20 будет 20 таких отрезков.
С этим фактом, вроде, никто не спорил.
Продолжим.
Теперь выясним, как связано число отрезков (или номер рисунка) с числом треугольников. Для этого нужно посчитать число треугольников в первых трех случаях по правилам, сформурированным на основе анализа вводного рисунка к задаче.
1 отрезок – 3 треугольника
2 отрезка – 6 треугольников
3 отрезка – 10 треугольников
Явной закономерности не видно. Нужно анализировать дальше.
Возвращаемся к первому поясняющему рисунку. Как там было получено 3 треугольника? Они получены суммированием двух групп треугольников, каждая из которых имеет общий отличительный признак – одинаковое число других треугольников внутри.
Одна группа – внутри которых нет других треугольников (т.е. число внутренних треугольников равно нулю). Таких треугольников 2. Вот эта группа. Вторая группа – внутри есть два треугольника. Таких треугольников 1. Соовтветственно, общее число треугольников подсчитывается по алгоритму:
2+1
Рассматриваем рис. 2. На этом рисунке можно выделить три группы треугольников:
В первой группе внутри треугольников нет, во второй группе внутри 2 треугольника, в третьей группе внутри три треугольника.
Группа 1 – 3 треугольника Группа 2 – 2 треугольника Группа 3 - 1 треугольник Сумарное число треугольников: 3+2+1
Анализируем рисунок.
По каким правилам подсчитываются треугольники:
1. Треугольник формируется из трех отрезков (эти отрезки выделены на поясняющем рисунке справа). Они формируют три стороны треугольника.
2. Внутри треугольника могут быть другие треугольники (пример – большой треугольник)
3. Подсчитываются всё возможные треугольники. Этот вывод делается на основании того, что в поясняющем рисунке подсчитаны именно все возможные треугольники (там всего три возможных, три посчитаны)
Теперь переходим к задаче.
Очевидно, что трем сформулированным выше правилам нужно подсчитывать треугольники на остальных рисунках (рис. 2, рис. 3, рис. 20). Ручной подсчет перебором на 20-м рисунке, в принципе, возможен, но очень трудоемок и за отведенное время явно не реализуем. Нужно сначала на основании первых сравнительно простых случаев увидеть эту закономерность.
Сначала проанализируем три первых рисунка выявить закономерность и понять, как будет выглядеть 20-й рисунок. Определим, что меняется. Внешний контур не меняется. Цвет не меняется. Убираем всё, что было постоянно и остается разница. Вывод: первый, второй и третий рисунок отличаются исключительно числом отрезков, соединяющих вершину треугольника с противолежашей стороной. Никаких других отличий нет.
Рис. 1 – 1 отрезок, рис. 2 – 2 отрезка, рис. 3 – 3 отрезка. Соответственно, на рис. 20 будет 20 таких отрезков.
С этим фактом, вроде, никто не спорил.
Продолжим.
Теперь выясним, как связано число отрезков (или номер рисунка) с числом треугольников. Для этого нужно посчитать число треугольников в первых трех случаях по правилам, сформурированным на основе анализа вводного рисунка к задаче.
1 отрезок – 3 треугольника
2 отрезка – 6 треугольников
3 отрезка – 10 треугольников
Явной закономерности не видно. Нужно анализировать дальше.
Возвращаемся к первому поясняющему рисунку. Как там было получено 3 треугольника? Они получены суммированием двух групп треугольников, каждая из которых имеет общий отличительный признак – одинаковое число других треугольников внутри.
Одна группа – внутри которых нет других треугольников (т.е. число внутренних треугольников равно нулю). Таких треугольников 2. Вот эта группа. Вторая группа – внутри есть два треугольника. Таких треугольников 1. Соовтветственно, общее число треугольников подсчитывается по алгоритму:
2+1
Рассматриваем рис. 2. На этом рисунке можно выделить три группы треугольников:
В первой группе внутри треугольников нет, во второй группе внутри 2 треугольника, в третьей группе внутри три треугольника.
Группа 1 – 3 треугольника Группа 2 – 2 треугольника Группа 3 - 1 треугольник Сумарное число треугольников: 3+2+1
- Aml
- Сообщения: 16662
- Зарегистрирован: 23 окт 2004, 00:10
- Настоящее имя: Сергей Амелин
- Откуда: Смоленск, Николаева
- Благодарил (а): 1 раз
- Поблагодарили: 59 раз
Re: Задачка по математике. 3 класс.
Анлогично для рисунка 3. Только там уже будет 4 группы треугольников
Группа 1 – 4 треугольника Группа 2 – 3 треугольника Группа 3 – 2 треугольника Группа 4 – 1 треугольник Суммарное число теугольников 4+3+2+1
Вот теперь закономерность явно видна. Номер рисунка с числом треугольников связан следующим образом:
1 – 2+1
2 – 3+2+1
3 – 4+3+2+1
Соответственно для 20-го рисунка число треугольников:
21+20+19+18+17+16+15+14+13+12+11+10+9+8+7+6+5+4+3+2+1=231
Получается, что условие задачи абсолютно корректно, оно не допускает множественности решения.
Для решения задачи используется лишь простейшая арифметика и простейшая логика. Плюс умение выявлять закономерности. Поэтому она вполне посильна третьеклассникам. А вот что намудоил составитель задачи с ответом – это большой вопрос. Но это не проблема условия задачи.
Отличительным признаком, позволяющим формировать группы треугольников, может быть не только число внутренних треугольников, но и число внутренних отрезков. Конечный результат т будет тот же самый.
Группа 1 – 4 треугольника Группа 2 – 3 треугольника Группа 3 – 2 треугольника Группа 4 – 1 треугольник Суммарное число теугольников 4+3+2+1
Вот теперь закономерность явно видна. Номер рисунка с числом треугольников связан следующим образом:
1 – 2+1
2 – 3+2+1
3 – 4+3+2+1
Соответственно для 20-го рисунка число треугольников:
21+20+19+18+17+16+15+14+13+12+11+10+9+8+7+6+5+4+3+2+1=231
Получается, что условие задачи абсолютно корректно, оно не допускает множественности решения.
Для решения задачи используется лишь простейшая арифметика и простейшая логика. Плюс умение выявлять закономерности. Поэтому она вполне посильна третьеклассникам. А вот что намудоил составитель задачи с ответом – это большой вопрос. Но это не проблема условия задачи.
Отличительным признаком, позволяющим формировать группы треугольников, может быть не только число внутренних треугольников, но и число внутренних отрезков. Конечный результат т будет тот же самый.
- hodok
- Сообщения: 16783
- Зарегистрирован: 01 фев 2007, 16:36
- Откуда: отсюда
- Благодарил (а): 0
- Поблагодарили: 0
Re: Задачка по математике. 3 класс.
Aml, допиши в последнее равенство недостающие слагаемые... 
А вообще,обсуждение задачки показательно .....его бы в тему про реформу образования
А вообще,обсуждение задачки показательно .....его бы в тему про реформу образования
- Aml
- Сообщения: 16662
- Зарегистрирован: 23 окт 2004, 00:10
- Настоящее имя: Сергей Амелин
- Откуда: Смоленск, Николаева
- Благодарил (а): 1 раз
- Поблагодарили: 59 раз
Re: Задачка по математике. 3 класс.
Блин, куда ж они делись... ДописалAml, допиши в последнее равенство недостающие слагаемые...
- Aml
- Сообщения: 16662
- Зарегистрирован: 23 окт 2004, 00:10
- Настоящее имя: Сергей Амелин
- Откуда: Смоленск, Николаева
- Благодарил (а): 1 раз
- Поблагодарили: 59 раз
Re: Задачка по математике. 3 класс.
Dms, а можно им (составителям задачи) на сайт передать то, что я тут наваял? Может им интересно будет 
-
John Watson
- Сообщения: 2657
- Зарегистрирован: 07 май 2010, 00:04
- Благодарил (а): 0
- Поблагодарили: 0
Re: Задачка по математике. 3 класс.
Первые три числа в правильном, по мнению составителя, ответе:
[3, 6, 10, x].
Неверные варианты четвёртого числа, по мнению составителя:
1, 21, 22, 210, 229, 231, 253.
Какие ещё варианты проверить?
[3, 6, 10, x].
Неверные варианты четвёртого числа, по мнению составителя:
1, 21, 22, 210, 229, 231, 253.
Какие ещё варианты проверить?
Последний раз редактировалось John Watson 26 фев 2016, 22:14, всего редактировалось 2 раза.
- John Prick
- Сообщения: 9367
- Зарегистрирован: 12 янв 2006, 19:30
- Благодарил (а): 431 раз
- Поблагодарили: 312 раз
- Контактная информация:
Re: Задачка по математике. 3 класс.
John Watson, может, он по аналогии с прямоугольниками посчитал? Проверь 210.
-
John Watson
- Сообщения: 2657
- Зарегистрирован: 07 май 2010, 00:04
- Благодарил (а): 0
- Поблагодарили: 0
Re: Задачка по математике. 3 класс.
John Prick, не, тогда первые три числа будут другими. 210 — неверный ответ.
Хотя, я допускаю, что просто ошибка (возможно, умышленная). В конце баллы участникам пересчитают
Хотя, я допускаю, что просто ошибка (возможно, умышленная). В конце баллы участникам пересчитают
- Aml
- Сообщения: 16662
- Зарегистрирован: 23 окт 2004, 00:10
- Настоящее имя: Сергей Амелин
- Откуда: Смоленск, Николаева
- Благодарил (а): 1 раз
- Поблагодарили: 59 раз
Re: Задачка по математике. 3 класс.
[3, 6, 10, 1].Какие ещё варианты проверить?
Там в условии задачи на 20 рисунке только один треугольник нарисован. И спрашивается, сколько треугольников на каждом рисунке
- Aml
- Сообщения: 16662
- Зарегистрирован: 23 окт 2004, 00:10
- Настоящее имя: Сергей Амелин
- Откуда: Смоленск, Николаева
- Благодарил (а): 1 раз
- Поблагодарили: 59 раз
Re: Задачка по математике. 3 класс.
Если первые числа ответа [3, 6, 10] признаны правильными, то алгоритм, который мы тут рассматривали также правильный.
Единственно возможный вывод: четвертое число ответа в базе сайта ошибочное. Случайно ли в базу попал неправильный ответ или преднамеренно, это уже детали...
Единственно возможный вывод: четвертое число ответа в базе сайта ошибочное. Случайно ли в базу попал неправильный ответ или преднамеренно, это уже детали...
- Sash
- Сообщения: 8491
- Зарегистрирован: 21 июл 2009, 17:17
- Откуда: смоленск
- Благодарил (а): 0
- Поблагодарили: 21 раз
- Контактная информация:
Re: Задачка по математике. 3 класс.
Да всё верно...и 231 для треугольников...и 210 для прямоугольников... Я для треугольников чисто арифметически вроде сделал алгоритм для общего случая...S = 3N+(N-2)+(N-3)+(N-4)...где N - число делящих отрезков и (N-Х) - неотрицательное число...эта же формула подходит и для задачи с прямоугольниками только с прибавлением 1 (для первого неподеленного прямоугольника) и началом отсчета со второго прямоугольника...John Prick писал(а):John Watson, может, он по аналогии с прямоугольниками посчитал? Проверь 210.
- Dms
- Сообщения: 8391
- Зарегистрирован: 15 ноя 2006, 23:43
- Настоящее имя: Серёга
- Откуда: Смоленск
- Благодарил (а): 29 раз
- Поблагодарили: 29 раз
- Контактная информация:
Re: Задачка по математике. 3 класс.
Блин, много я пропустил сегодня. Через 20 минут мы узнаем подходит ли один из предложенных тут вариантов.
Американская фирма Transceptor Technology
Приступила к производству компьютеров "Персональный спутник"
Приступила к производству компьютеров "Персональный спутник"
- Dms
- Сообщения: 8391
- Зарегистрирован: 15 ноя 2006, 23:43
- Настоящее имя: Серёга
- Откуда: Смоленск
- Благодарил (а): 29 раз
- Поблагодарили: 29 раз
- Контактная информация:
Re: Задачка по математике. 3 класс.
Вариант 3-4-5-22 - 1 балл из 10, 3-6-10-231 - 4 балла из 10.....
Американская фирма Transceptor Technology
Приступила к производству компьютеров "Персональный спутник"
Приступила к производству компьютеров "Персональный спутник"
- Dms
- Сообщения: 8391
- Зарегистрирован: 15 ноя 2006, 23:43
- Настоящее имя: Серёга
- Откуда: Смоленск
- Благодарил (а): 29 раз
- Поблагодарили: 29 раз
- Контактная информация:
Re: Задачка по математике. 3 класс.
У меня идеи кончились...
Американская фирма Transceptor Technology
Приступила к производству компьютеров "Персональный спутник"
Приступила к производству компьютеров "Персональный спутник"
-
Мистер Смитт
- Сообщения: 14072
- Зарегистрирован: 17 мар 2008, 11:27
- Настоящее имя: Олег
- Откуда: Смоленск
- Благодарил (а): 0
- Поблагодарили: 0
- Контактная информация:
Re: Задачка по математике. 3 класс.
... бред, это 3 класс !Dms писал(а):Вариант 3-4-5-22 - 1 балл из 10, 3-6-10-231 - 4 балла из 10.....
... во всём виноват Вашингтон поц ...
... следуй своей дорогой и пусть люди говорят всё что угодно ...
... следуй своей дорогой и пусть люди говорят всё что угодно ...
- Dms
- Сообщения: 8391
- Зарегистрирован: 15 ноя 2006, 23:43
- Настоящее имя: Серёга
- Откуда: Смоленск
- Благодарил (а): 29 раз
- Поблагодарили: 29 раз
- Контактная информация:
Re: Задачка по математике. 3 класс.
Мистер Смитт, твой вариант ? Проверим?
Американская фирма Transceptor Technology
Приступила к производству компьютеров "Персональный спутник"
Приступила к производству компьютеров "Персональный спутник"
- John Prick
- Сообщения: 9367
- Зарегистрирован: 12 янв 2006, 19:30
- Благодарил (а): 431 раз
- Поблагодарили: 312 раз
- Контактная информация:
Re: Задачка по математике. 3 класс.
Dms, а там только сам ответ да кол-во баллов влияет? Может, для большего числа баллов ответ надо как-то обосновать, только сайт не позволяет технически это.У меня идеи кончились...
- John Prick
- Сообщения: 9367
- Зарегистрирован: 12 янв 2006, 19:30
- Благодарил (а): 431 раз
- Поблагодарили: 312 раз
- Контактная информация:
Re: Задачка по математике. 3 класс.
Тут подумалось, 3 класс - это ведь 9-10 лет. Дети в это время в шахматы, например, играют уже в силу 1го разряда. Это уже очень прилично. Причём играют почти все, кто начал заниматься ими лет в 7-8. Т.е. это не феномен, а закономерность. Так то шахматы, сложная игра, а тут какие-то треугольнички.... бред, это 3 класс !
-
Shador
- Сообщения: 10867
- Зарегистрирован: 01 мар 2010, 14:15
- Благодарил (а): 686 раз
- Поблагодарили: 1677 раз
Re: Задачка по математике. 3 класс.
докину еще вариант решения:Aml писал(а):Dms, а можно им (составителям задачи) на сайт передать то, что я тут наваял? Может им интересно будет
количество всех возможных треугольников будет равно количеству всех возможных сочетаний по два (без учета порядка) отрезков, проведенных из вершины треугольника к его основанию (включая стороны).
тогда общая формула количества сочетаний С=n!/m!(n-m)! применительно к исчисляемым треугольникам будет иметь вид:
С=n!/2!(n-2)!, где n - число отрезков, включая стороны.
упростив ее, получим: С=n*(n-1)/2
на 20-м рисунке будет 22 отрезка, соответственно число треугольников равно:
22*21/2=11*21=231
-
Shador
- Сообщения: 10867
- Зарегистрирован: 01 мар 2010, 14:15
- Благодарил (а): 686 раз
- Поблагодарили: 1677 раз
Re: Задачка по математике. 3 класс.
п.с. ребенок мог бы увидеть такую закономерность: каждый новый добавленный отрезок добавляет на рисунке количество треугольников, равное числу отрезков на рисунке перед добавлением.
-
Storm
- Сообщения: 4784
- Зарегистрирован: 19 ноя 2004, 11:44
- Откуда: Smolensk
- Благодарил (а): 0
- Поблагодарили: 3 раза
- Контактная информация:
Re: Задачка по математике. 3 класс.
А что, досрочно завершить нельзя? Нужно 30 минут ждать в любом случае?
- Dms
- Сообщения: 8391
- Зарегистрирован: 15 ноя 2006, 23:43
- Настоящее имя: Серёга
- Откуда: Смоленск
- Благодарил (а): 29 раз
- Поблагодарили: 29 раз
- Контактная информация:
Re: Задачка по математике. 3 класс.
Storm, если найдешь способ досрочно завершить, мы им сайт положим перебором решений )))
Американская фирма Transceptor Technology
Приступила к производству компьютеров "Персональный спутник"
Приступила к производству компьютеров "Персональный спутник"
-
Мистер Смитт
- Сообщения: 14072
- Зарегистрирован: 17 мар 2008, 11:27
- Настоящее имя: Олег
- Откуда: Смоленск
- Благодарил (а): 0
- Поблагодарили: 0
- Контактная информация:
Re: Задачка по математике. 3 класс.
... я же давно написал - 22, один баллDms писал(а):Мистер Смитт, твой вариант ? Проверим?
... во всём виноват Вашингтон поц ...
... следуй своей дорогой и пусть люди говорят всё что угодно ...
... следуй своей дорогой и пусть люди говорят всё что угодно ...
